Para entendermos o Paradigma Procedimental é interessante que vejamos, antes, o que são procedimentos. Para isso, considere o problema de escrever um algoritmo que lê um número inteiro n e calcula o seu fatorial. Podemos chegar ao seguinte programa:
[wptabs mode=”horizontal”]
[wptabtitle]C#[/wptabtitle]
[wptabcontent]
[code language=”csharp” highlight=”4,5,6,7,8″]
Console.Write("n: ");
int n = int.Parse(Console.ReadLine());
int fatorial = 1;
for (int i = 1; i <= n; i++)
{
fatorial = fatorial * i;
}
Console.WriteLine("n! = {0}", fatorial);
[/code]
[/wptabcontent]
[wptabtitle]Java[/wptabtitle]
[wptabcontent]
[code language=”java” highlight=”6,7,8,9″]
Scanner console = new Scanner(System.in);
System.out.print("n: ");
int n = Integer.parseInt(console.nextLine());
int fatorial = 1;
for (int i = 1; i <= n; i++) {
fatorial = fatorial * i;
}
System.out.printf("n! = %d\n", fatorial);
[/code]
[/wptabcontent]
[/wptabs]
Percebemos que as linhas destacadas é que fazem o processamento. As outras cuidam da entrada/saída de dados de/para o usuário.
Agora, considere o problema de escrever um algoritmo que calcula a quantidade de diferentes combinações que podem ser feitas com n elementos agrupados k a k. A fórmula para esse cálculo é [latex]C(n, k) = \frac{n!}{k!(n-k)!}[/latex]. Nesse caso, podemos chegar ao seguinte programa:
[wptabs mode=”horizontal”]
[wptabtitle]C#[/wptabtitle]
[wptabcontent]
[code language=”csharp” highlight=”7,8,9,10,11,13,14,15,16,17,19,20,21,22,23″]
Console.Write("n: ");
int n = int.Parse(Console.ReadLine());
Console.Write("k: ");
int k = int.Parse(Console.ReadLine());
int fatorialN = 1;
for (int i = 1; i <= n; i++)
{
fatorialN = fatorialN * i;
}
int fatorialK = 1;
for (int i = 1; i <= k; i++)
{
fatorialK = fatorialK * i;
}
int fatorialNK = 1;
for (int i = 1; i <= (n – k); i++)
{
fatorialNK = fatorialNK * i;
}
int c = fatorialN / (fatorialK * fatorialNK);
Console.WriteLine("C({0}, {1}) = {2}", n, k, c);
[/code]
[/wptabcontent]
[wptabtitle]Java[/wptabtitle]
[wptabcontent]
[code language=”java” highlight=”9,10,11,12,14,15,16,17,19,20,21,22″]
Scanner console = new Scanner(System.in);
System.out.print("n: ");
int n = Integer.parseInt(console.nextLine());
System.out.print("k: ");
int k = Integer.parseInt(console.nextLine());
int fatorialN = 1;
for (int i = 1; i <= n; i++) {
fatorialN = fatorialN * i;
}
int fatorialK = 1;
for (int i = 1; i <= k; i++) {
fatorialK = fatorialK * i;
}
int fatorialNK = 1;
for (int i = 1; i <= (n – k); i++) {
fatorialNK = fatorialNK * i;
}
int c = fatorialN / (fatorialK * fatorialNK);
System.out.printf("C(%d, %d) = %d\n", n, k, c);
[/code]
[/wptabcontent]
[/wptabs]
Abstrações, Encapsulamento e Procedimentos
Aqui podemos perceber, pelas linhas destacadas, que o algoritmo do primeiro problema aparece três vezes dentro do algoritmo do segundo problema. Isso nos leva às seguintes observações:
- Para eu escrever o algoritmo do cálculo de combinações, tive que escrever três vezes o mesmo algoritmo do fatorial, ou seja, foi difícil (impossível) de expressar que o que eu realmente queria era calcular o fatorial de um número. Além disso, não foi possível reusá-lo, tendo que escrever o mesmo conjunto de linhas em locais diferentes.
- De forma semelhante, se eu fosse tentar entender o algoritmo do cálculo de combinações, teria que notar que existe um conjunto de linhas que se repetem de alguma forma; e, analisando melhor, veria que cada um desses conjuntos é, na verdade, um outro algoritmo que calcula o fatorial de um número.
- Se, por algum motivo, eu precisar alterar o algoritmo do fatorial (acrescentando, por exemplo, uma verificação que impedisse o cálculo para número negativos) eu teria que fazer modificações em três locais distintos do meu algoritmo do cálculo de combinações.
Diante dessas observações, dizemos que as linhas destacadas são abstrações para o algoritmo do fatorial. Abstrações são partes de um todo que podem ser estudadas de forma isolada. É quando podemos nos concentrar somente nessa parte do algoritmo e nos esquecer das outras partes. Um exemplo de abstração é quando estudamos o corpo humano. Nós não o estudamos como um todo e sim em partes separadas: o sistema circulatório, o respiratório, o nervoso, etc. Cada um desses sistemas é uma abstração do corpo humano, ou seja, podemos estudá-los isoladamente. Dividimos um sistema complexo (o corpo humano) em sistemas mais simples de serem entendidos.
É interessante notar que, muitas vezes, ao escrevermos um programa, usamos linhas em branco para isolar alguns conjuntos de linhas de código pois elas fazem sentido juntas. Fazer isso é um comportamento que mostra que estamos tentando demarcar abstrações, mas estamos sem um mecanismo apropriado para isso.
Assim, o que nos falta nesse momento é um mecanismo para isolar a abstração do algoritmo do fatorial de dentro do algoritmo do cálculo de combinações. O Paradigma Procedimental nos fornece esse mecanismo: ele é chamado de procedimento. Ou seja, podemos dizer que procedimento é um mecanismo para encapsular uma abstração.
Outra forma de entender procedimento é considerá-lo como sendo um algoritmo que é usado por outros algoritmos e, por isso, suas entradas e saídas não estão relacionadas com o usuário e sim com o algoritmo que vai usá-lo. E é por isso que, muitas vezes, um procedimento também é chamado de sub-algoritmo.
Agora que já conhecemos o que são abstrações, encapsulamento, procedimentos, etc. podemos resolver o segundo problema da seguinte forma:
[wptabs mode=”horizontal”]
[wptabtitle]C#[/wptabtitle]
[wptabcontent]
[code language=”csharp” highlight=”9,14,15,16,17,18,19,20,21,22″]
public static void Main(string[] args)
{
Console.Write("n: ");
int n = int.Parse(Console.ReadLine());
Console.Write("k: ");
int k = int.Parse(Console.ReadLine());
int c = fatorial(n) / (fatorial(k) * fatorial(n – k));
Console.WriteLine("C({0}, {1}) = {2}", n, k, c);
}
public static int fatorial(int n)
{
int fatorial = 1;
for (int i = 1; i <= n; i++)
{
fatorial = fatorial * i;
}
return fatorial;
}
[/code]
[/wptabcontent]
[wptabtitle]Java[/wptabtitle]
[wptabcontent]
[code language=”java” highlight=”10,15,16,17,18,19,20,21″]
public static void main(String[] args) {
Scanner console = new Scanner(System.in);
System.out.print("n: ");
int n = Integer.parseInt(console.nextLine());
System.out.print("k: ");
int k = Integer.parseInt(console.nextLine());
int c = fatorial(n) / (fatorial(k) * fatorial(n – k));
System.out.printf("C(%d, %d) = %d\n", n, k, c);
}
public static int fatorial(int n) {
int fatorial = 1;
for (int i = 1; i <= n; i++) {
fatorial = fatorial * i;
}
return fatorial;
}
[/code]
[/wptabcontent]
[/wptabs]
Detalhes sobre Procedimentos
Podemos notar, na primeira linha destacada, o uso (ou chamada) do procedimento que calcula o fatorial de um número. A chamada de um procedimento tem a seguinte formação:
fatorial: nome do sub-algoritmo que se quer executar.(...): uma lista de valores que servirão como dados de entrada; os parênteses são obrigatórios, mesmo no caso do sub-algoritmo a ser executado não precisar de dados de entrada.
Mais abaixo, nas últimas linhas destacadas, está a criação do procedimento, que é feita da seguinte forma:
public: usado para que nosso sub-algoritmo possa ser acessado de qualquer lugar do nosso algoritmo.static: nas linguagens usadas, servem para dizer que estamos usando o Paradigma Procedimental (isso não é bem verdade, mas é como se fosse; em outro post irei definir exatamente o que significa ostatic).int: é o tipo de dado da saída desse sub-algoritmo.fatorial: é o nome do sub-algoritmo.(int n): lista de variáveis que receberão os dados de entrada desse sub-algoritmo; também é chamado de parâmetros do procedimento.{ ... return fatorial; ... }: o sub-algoritmo em si vai dentro de chaves; o que é importante aqui é o comandoreturn, que faz a saída do sub-algoritmo, retornando o valor para o algoritmo que o está chamando. Notar que esse comando encerra a execução do procedimento.
É importante deixar claro que o algoritmo principal faz três chamadas ao sub-algoritmo fatorial (na mesma linha de código). Em cada uma dessas vezes ele envia (ou passa) um argumento (valor) diferente para o parâmetro (variável) n.
- Na primeira vez o argumento passado é o valor da variável n do algoritmo principal.
- Na segunda vez, o argumento passado é o valor da variável k do algoritmo principal.
- Na terceira vez, o argumento passado é o valor da operação n – k, onde n e k são variáveis do algoritmo principal.
Em todas as vezes, é o parâmetro n do sub-algoritmo fatorial é que recebe o valor do argumento passado. Assim, existem duas variáveis n: uma no algoritmo principal e outra no sub-algoritmo fatorial. Isso é possível porque elas estão em escopos diferentes, ou seja, estão em algoritmos diferentes. Cada vez que o algoritmo principal chama o sub-algoritmo fatorial, ele é executado de forma independente das outras execuções e sua variável n recebe o novo valor sendo passado.
Conclusão
Voltando à questão do Paradigma Procedimental, ao compararmos os dois algoritmos para cálculo de combinações, fica claro que, ao usarmos procedimentos, ganhamos em:
- Expressividade no momento de escrever os algoritmos.
- Clareza no entendimento dos mesmos.
- Capacidade de reuso de suas partes.
- Flexibilidade em alterá-los.
E a forma de pensar, de construir um algoritmo, muda em relação ao Paradigma Estruturado: agora, o nosso algoritmo passa a ser formado por um conjunto de procedimentos onde a saída de um é passada como entrada para outro; e cada um deles pode ser formado por vários outros procedimentos. A figura abaixo ilustra essa situação:
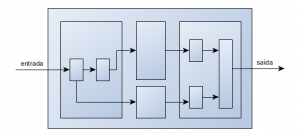
O algoritmo passa a ser formado por um conjunto de procedimentos onde a saída de um é passada como entrada para outro; e cada um deles pode ser formado por vários outros procedimentos.
Agora, passamos a ter que pensar em como dividir nosso problema em problemas menores que serão resolvidos, cada um, por um pequeno algoritmo específico, simples de escrever, entender, reusar e alterar. Dividir para conquistar é o lema.
Será que, após a leitura desse post, você consegue fazer, facilmente, um algoritmo que imprime o Triângulo de Pascal? A resposta, bem como os programas apresentados aqui, encontram-se em:
Antes de finalizar esse post de fato, quero fazer algumas observações muito importantes:
- Vejo muita gente dizer Paradigma Procedural ao invés de Procedimental. Provavelmente isso ocorre porque procedimento, em Inglês, é procedure. Aí, quando trazemos esse termo para o Português, fica procedural. Mas, por favor, use o termo procedimental que soa muito melhor! 🙂
- Você provavelmente já viu, nos seus estudos, o termo função ser usado no lugar de procedimento, assim como eu usei o termo procedimento em todo esse post, indistintamente. Ocorre que, academicamente, existe uma diferença: a função retorna algum valor enquanto que o procedimento não; assim, no exemplo que eu dei, fatorial não é exatamente um procedimento, e sim uma função. De qualquer maneira, para ser didático, também usarei os dois termos indistintamente.
- Existem diversos tópicos sobre procedimentos que não foram abordados nesse post até porque fogem da questão de paradigmas de programação; entre esses tópicos estão: passagem de argumentos por valor (ou cópia) e por referência, recursividade, entre outros.
Prezado Ramon,
1. Este paradigma procedimental constituiria uma estratégia de dividir o problema a ser resolvido, em problemas menores e, então, desenvolver os algoritmos? Seria aquela estratégia (Divide and Conquer).
2. Minha primeira dúvida antes de ler todo o post foi em relação à variável n. Eu a vi sendo declarada no main, juntamente com as variáveis k e c e, depois, a vi sendo utilizada no sub-algoritmo fatorial. Isso me gerou uma dúvida, que logo foi sanada com a leitura completa do artigo. Mas, permaneceu uma dúvida: porque no método “public static int fatorial(int n)” não houve a declaração desta segunda variável “n” antes dela ser usada no laço for. Ou, melhor dizendo, ela é inicializada justamente quando utilizada no for?
Grande abraço!
Grande Emmanuel,
1. Sim, é a estratégia “Dividir para Conquistar”. Mas, isso não é usado apenas quando estamos no paradigma procedimental. No orientado o objetos também existe essa mentalidade! Em geral, quando programamos, temos que resolver problemas muito complexos. Aí, precisamos dividir esse problema em problemas menores, mais simples. Isso pode ser feito por meio de procedimentos/funções ou classes, dependendo do paradigma.
2. A variável “n” que está no sub-algoritmo “fatorial” está declarada na lista de parâmetros dela! Quando criamos uma lista de parâmetros, estamos, na verdade, criando uma lista de variáveis que vão receber os valores passados como entrada.
Espero que tenha ajudado!
Grande abraço para você, também!!!